Is there a calculation comparing acceleration of one unicycle to another

General
1

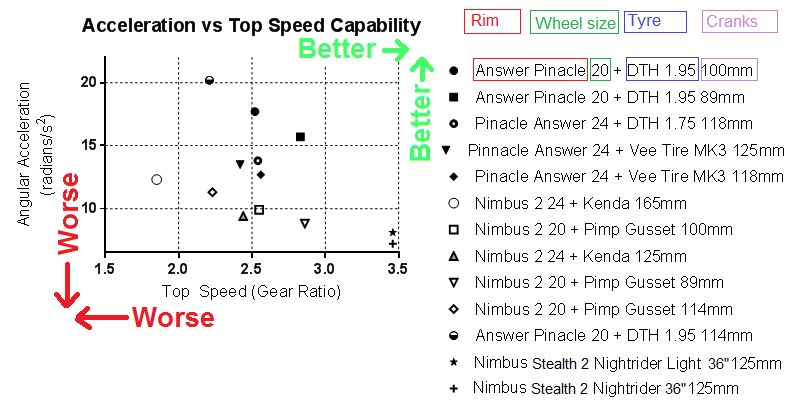
I’m trying to figure out the important variables to consider when comparing different unicycle sizes. By reading through other posts, I’ve stumbled across: velocity, gear ratio, and acceleration.

Velocity
When trying to compare one unicycle size to another, other posts talk about the relationship between wheel size, cadence and velocity (velocity = cadence X wheel circumference). I understand that for a given RPM a larger wheel is going to go faster.

Gear Ratio
I love this post with a table on gear ratios: http://195.66.135.134/forums/showthread.php?t=88333

Acceleration
Other posts mention that in order to compare one unicycle size to another, it’s not just about velocity. You also need to account for how quickly a unicycle can accelerate/decelerate, which depends on wheel size, the mass of the wheel, and crank length. So, a relative acceleration calculation would be helpful (but it’s not as easy as the velocity calculation).

Are there any posts that discuss how to calculate the acceleration? I’ve done a calculation, but would like to see other posts before I post something redundant. A quick five minute search did not uncover anything.

What other variables are important?
Is there anything else to be considered?

Maybe a calculation on how easy it is for a given unicyle size to maintain a cruising velocity? I’m guessing this would be: Sum of Forces = mass X acceleration = Zero (because you are not accelerating at a constant velocity). So, the wind resistance + bearing friction + static friction force from the wheel on ground would have to equal the torqe from pedaling. The variables involved would be 1) mass of the rider+unicycle, 2) wheel size, 3) crank length, 4) drag coef of a bicyclist has to be posted somewhere, 5) coef of friction of tire on dirt or road is out there somewhere, 6) I’d ignore bearing friction.

Sorry for geeking out on you!

2

By far the largest and most important variable, which you have not included in your list, is the rider. That one variable makes all the others essentially meaningless.

3

Very true!! But, since I’m the only rider that I care about when trying to figure out what unicycle to buy, I cancel myself out…:wink:

4

You’re over-thinking this. A unicycle is not a physics problem; the number of variables in the real-world speed of a rider is far larger than can be calculated by formula.

Lighter unicycles accelerate faster (and you’re always accelerating something, as long as your wheel is spinning). But if you measure the same rider in the same conditions 10 times, you’ll get 10 different results on acceleration speed, and those results will be pretty significantly divergent.

5

I completely agree, Tholub… I am totally over thinking this. Actually, I should be banished to the nerds’ area of the forum.

At this point, I’m really just doing this for fun. Josh at Unicycle.com has me all set up with a new Drac 29".

It’s just that I enjoy theoretical problems and can’t seem to let this go. I’m hoping there are some mechanical engineering profs. or physicists on the thread that can whip this out.

6

There are plenty of mechanical engineers and physicists here. That won’t help with a system whose primary component is implemented in a bewildering array of poorly-specified materials.

7

I’m not looking for any absolute acceleration values. I’m just trying to compare one unicycle size to another.

Angular form of Newton’s 2nd law is:
T = I * α

where
T is torque,
I is mass moment of inertia,
α is angular acceleration.

The torque is equal to the force your foot applies to the pedal times the crank arm length:
T = F * r

where
F is force applied by your foot on the pedal,
r is the crank length.

So,
F * r = I * α ===> F = I * α / r

Ok, now here is where I think my logic may be off and could use some help. I think that in order to compare unicycle A to unicycle B, you would want to look at the acceleration of each unicycle for the same force applied by your foot on the pedal, F.

So,
Ia * αa / ra = Ib * αb / rb

where
Ia = mass moment of innertia of the wheel on unicycle A
Ib = mass moment of innertia of the wheel on unicycle B
αa = angular acceleration of unicycle A
αb = angular acceleration of unicycle B
ra = crank length on unicycle A
rb = crank length on unicycle B

In order to compare the relative accelerations of each unicycle rearrange the equation like this:
αa/αb = Ib/Ia * ra/rb

Now, the mass moment of inertia for a wheel (let’s ignore the cranks and pedals just for simplicity) is equal to:
I = m * R^2

where
m = mass of the wheel
R = wheel radius

So, the final equation is:
αa/αb = (mb * Rb^2) / (ma * Ra^2) * (ra/rb)
= (mb/ma) * (Rb^2 / Ra^2) * (ra/rb)

I used this equation to try to compare the Nimbus 29” Drac with the Nimbus 26” Muni:

Unicycle A: (26” muni)
Mass of the Nimbus 26” wheel, tire, and stock cranks = 4.3 kg (due to heavy tire)
Stock crank length = 165 mm
Radius of 26” wheel = 330.2 mm

Unicycle B: (29” Drac)
Mass of the Nimbus 29” wheel, tire, and stock cranks = 3.7 kg
Stock crank lengths = 165 mm.
Radius of 29” wheel = 368.3 mm

So,
αa/αb = (3.7/4.3) * (368.3^2 / 330.2^2) * (165/165) = 1.07

So, I think that this is saying that the 26” muni would only accelerate 7% faster than the 29” drac. Again, not quite sure about this logic.

8

I am positive about this logic.

9

If the 29er has a lighter rim and tire, it will accelerate faster than the 26", so even leaving aside the fact that the math you’re doing is meaningless, your math is wrong.

10

The nerds’ area is called unicyclist.com. :stuck_out_tongue:

But to geek out a little, if you pretend all your comparison unicycles have the same type rim and tire (and spokes, cranks, pedals, etc.) it can add some meaning to your math. But it can’t be translated to real unicycles since you usually won’t get the same rim or tire in all those different sizes.

11

Physicist here. I’d just like to point out that your calculations are meaningless until you include margins of error.

See: Propagation of uncertainty - Wikipedia

You ride them both then buy the one you like best.

If you don’t have the ability to ride both, then just buy one and save money for the other. Eventually you will own both.

This is the first law of unicycling: As t approaches infinity, so does the number of unicycles you will own.

12

I’m no physicist, not even an engineer, but that doesn’t keep me from posting :wink:

Okay, so you’re a nerd, obviously bored at work/school, but really, we’re talking about how fast a unicycle can accelerate? A turtle can accelerate faster than a unicycle!

The funniest thing for me was after completing a twenty mile mtb race on my uni, I looked at my time and the mileage/terrain covered and realized that I could have run that same race faster than I rode it :astonished:

So, with my apprentice engineers hat I have a couple thoughts:

A longer crank and more body weight/physcial strength, as well as having a handle that allows for increased leverage, these things will improve initial accelaration. All things held constant; same handle/crank size/tire design, a smaller and lighter uni will clearly be quicker to both start and stop.

That said, being quick on a uni has never been my problem, I’m more inclined to be concerned with duration of sustained effort, overall endurance, change in skill level/ability when fatigued, etc…

My goal is to build my skills and my muscles so that I can sustain longer rides at higher skill levels.

So why would you be interested in acceleration of a uni?

How about some studies regarding endurance riding and the effects of uni weight, crank length, wheel size, tire pattern, leg extension/bend, geared vs ungeared? This would all be very applicable and highly beneficial to me as a rider.

13

Again, everyone, thanks for the feedback!!!

I don’t care about the actual acceleration. I agree with you all. I also don’t care about margins of error (not concerned about an absolute answer). Also, I’ve completely ignored friction at the bearing and at the wheel/ground contact.

This all started as an exercise to help me decide between a 26" and 29" unicycle. Unfortunately, I don’t have the time/patience to track down unicycles to actually try. So, I thought a little calculation may help me decide. As a result, I stayed up way to late the other night digging out my dynamics book and working on the equations above. (Being extra tired the next morning is probably why I couldn’t ride straight: How much of being able to ride a unicycle is psychological? )

Here was my background logic. I know that wheel size has an obvious affect on velocity. I also know that crank length is the only economical control you have over gearing for a given wheel size. However, a statement was made on one other thread along the lines of, [it is not just crank length and wheel size that can cause one unicycle to feel so different than another. The mass of the wheel can also affect the feel.]

So, my point was more to understand (or account for) the impact of wheel mass. I thought that looking at how easily a unicycle could accelerate was the way to do this.

I think it was a useful exercise. With the same crank length, the 26" unicycle should accelerate faster. However, because of an extra heavy 3" wide tire on the 26" wheel, it was heavier than the 29". So, that offset the difference in wheel diameter and crank “gearing”.

My big assumption here is that more acceleration would provide more control over the unicycle. That’s got to play into why it’s easier for people to learn on a 20". Being a new rider with hardly any recent experience, this was just a guess.

Now, as some of you have pointed out, it’s time for me to forget about this and just go ride.

14

You’re ignoring the elephants. A 20 is easier to learn on because it’s lower (hence easier to get on and less scary when you’re up there), because it’s lighter (hence easier to throw around and less tiring) and because you go slower. To some extent, accelerating faster is a bad trait for learning as it results in less stability.

15

Then you must agree that 1 + 1 = 3.

Because, essentially, you could get such a result with large enough error bars… which your equation appears to have.

A picture for illustration.

num_line_margin_compare-yellow-ex.jpg
num_line_margin_compare-yellow-ex.jpg800×310 19.9 KB

16

Then there’s the “other” elephant. a 29" street-riding unicycle, with normal-sized or narrow wheel, is going to be great for riding down the street. A 26" with a 3" wide tire is going to be great for riding on the trails. Each will be lousy at doing the other. In other words, if you want to ride on dirt, you have to choose: Quick response in a light wheel with a harsh ride and limited lifespan, vs. slower response in a tire that can take the pounding, grip the dirt and mud, be much more comfortable to ride, and will last through much abuse. Acceleration isn’t really a factor.

A little. Not enough to matter for someone who’s learning to ride.

Here’s an example of when acceleration actually matters, the 100 meter final (men) at Unicon 12, at the Olympic stadium in Tokyo

17

For a very rough comparison between two unicycles you could take

[total weight (you and unicycle) + rotating weight] / gain ratio from chart = unitless number relating to acceleration potential of you on your unicycle.

Or if you are looking for just the potential for acceleration of the wheel without rider etc.

Rotating weight / gain ratio = potential wheel acceleration. (this number might be better for figuring out how much control you should theoretically have.

If you know the weights of the components you could figure rotating weight as roughly tire + rim + tube + .5spokes + petals/gain ratio + cranks/(2gain ratio)

EDIT: of course this will have very little bearing on how easy a unicycle is to ride in real life.

18

I thought this forum was for nerds, I am amazed at how dismissive everyone is of someone trying to calculate wheel characteristics of unicycles. No wonder the OP has only posted 25 times since 2012 when this was the reception to his first post.

ANYHOW for unicycle team sports (hockey) I have been eager to be able to compare wheel abilities for a while. I came to a similar conclusion to the OP that using inertia and total gear ratio was the way to go.

I believe the handling of a wheel in hockey is different to many other disciplines in that it is a game of fast acceleration/deceleration and turning meaning the ability to accelerate may be as or more important than top speed.
What I did

  1. Determined the total gear ratio from crank radius and inflated tyre radius. Used this as a proxy of potential for speed.
    2.Determined rough moment inertia of wheels using rim and tyre of setup and radius from the centre.
  2. Determined Torque based on a estimate of 80N (Crank length in meters * Newtons of force)
  3. Determined angular acceleration of the wheel setup. (Angular acceleration = torque/moment of inertia. Used the angular acceleration as the wheel ability to accelerate.
  4. Plotted this on a scatter graph to compare different wheel builds speed/acceleration potential.
    [/LIST]

The resulting graph shows that lighter rim/tyre combos make a big difference in acceleration ability, particularly that the stock nimbus 2 rim with Pimp Gusset tyre, a build that >70% in my country use and think is the best option is actually worse than a well built 24. It also shows the trade off in crank length for acceleration/top speed.

Assumptions:

  • I ignored spokes and hubs in this calculation as hubs are so small in radius and similar weights that for this rough attempt I don't think it matters. Spokes I have worked out previously and are tiny compared to rim/tyre. Worked out rim and tyre inertia based on radius of tyre (exception in the case of the 36") meaning the total inertia would be slightly lower for these setups as the rim has a smaller radius. I would add both hub and spokes in if I was going to take it super serious. This is a proof of concept not a final attempt at the best data that can be gained.
  • The Total gear ratio as a proxy for speed assumes that smaller cranks are able to be spun faster than longer cranks. If the smaller cranks are spun at the same cadence as the larger wheel then the larger would obviously have the higher speed. In this case someone on a 24" with 165mm cranks could go faster than someone on a 20" with 89mm cranks. Until I get some hard data that smaller cranks can be spun faster due to smaller circumference of the feet this is just an assumption.
  • Acceleration ability is important to hockey but may not be nearly as important for a rider in the marathon. As you can see on the list the nimbus nightrider has much higher TGR (and suprise suprise goes faster) and a much lower acceleration ability. A rider in a marathon is probably more keen on having high inertia to keep the wheel rolling than having it slow down so easily. For different disciplines you would look for different variables as desirable.
  • This is an assessment only of EQUIPMENT not the RIDER. I realise that an individual rider/their abilities/what crank length they are used to makes a difference to top speed. However I believe a given rider will always be able to accelerate a wheel faster when it has a lower inertia. Also performance characteristics make a difference, that is why track cycling is a game of numbers.

Calculations

Acceleration vs Top Speed Capability2.png
Acceleration vs Top Speed Capability2.png800×412 20.6 KB

19

What you completely forgot, is to factor in the weight of the rider. Even though it is a constant, I think it’s important to scale it, to put it in proportion. What we can see is how much more momentum one setup has compared to another, but I would like to see how much of a difference that makes overall, my guess would be that a 75 kg rider weight compared to 70 kg rider weight is going to be more of a difference than the best momentum of inertia you calculated compared to the worst moment of inertia.

I might add that calculation tomorrow.

20

This is a comparison of equipment irrespective of rider weight. If we are taking into account rider weight we may as well say if rider A can produce 80N and rider B can produce 200N rider B will accelerate faster whatever he is riding. Or if rider A can ride at 130RPM and rider B can ride at 200RPM then rider B will have a higher top speed no matter what his RPM. There is no real need to factor in rider weight for these calculations as this is about how two pieces of equipment will behave.

Taking into account frame weight is fair enough, however I think it is probably minor compared to the rotational inertia. Keen to see that info though, I assumed frame weight would be relatively minor compared to rotational weight in acceleration as usually the difficulty in acceleration is not moving your body forward but ensuring your feet can get your wheel moving fast enough, so ignored it.

If we take into account body composition I think most disciplines would benefit from a rider being as lean as possible with the highest strength to weight ratio as possible.