Sorry about the newbie question, but how does wheel size affect mechanical advantage on a unicycle? I understand that longer cranks increase leverage. However, if you hold crank length constant (e.g., 125 mm), would you gain a mechanical advantage by using a smaller wheel?
Yes you do. You would have better leverage with 125s on a 20 compared to 125s on 36er
rpt50,
Welcome to the forums.
The gear ratio (crank length/wheel diameter) is hugely important. Unicyclists can talk for hours about this. This might not be the most fascinating conversation you’ve ever witnessed, but everyone has their opinions. In fact, there are several threads devoted to this.
Here’s one: New concept: Total Gear Ratio
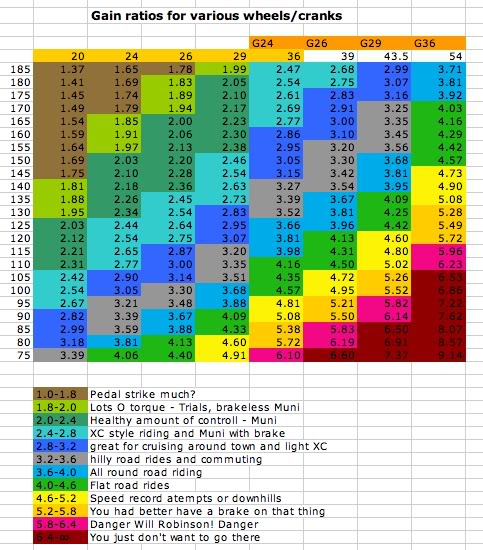
Saskatchewanian came up with this beautiful chart of all the different conceivable configurations of available crank lengths and wheel sizes and their resulting gear ratios. He even included the effective wheel diameters of geared 24", 26", 29" and 36" wheels. (Eric, I can’t help but mention that now you need to include the 32" wheel. Geared and ungeared, of course. :D)
Happy reading.
Geoff
Wow! Thanks for the info. That spreadsheet chart is awesome!
WOW!!
That is way impressive!
Thanks
This may be more than you wanted, but with help from the guys at a physics forum, I found a mathematical description the effects of wheel diameter/crank length:
Yes, smaller wheels offer a mechanical advantage.
The proper way to show it is by knowing that the torque at the crank © is the same as the torque at the wheel (w) (since they are part of the same unit):
Tc = Tw
Fc * Rc = Fw * Rw
or
Fw = Fc * Rc / Rw
Assuming the same force at the crank (Fc), the friction force acting between the ground and the tire (Fw) is inversely proportional to the wheel radius (Rw). The smaller the wheel, the larger the force.
Similarly, for speed (V), we know that the angular velocity (w) will be the same for the crank and the wheel:
wc = ww
Vc / Rc = Vw / Rw
or
Vw = Vc * Rw / Rc
Here, assuming the same speed at the crank (Vc), the velocity of the wheel at the ground (hence the unicycle velocity) is proportional to the wheel radius. The smaller the wheel, the lower the unicycle speed.
By changing the wheel or crank radius, you gain force and loose speed (or vice versa).
If you want to know how much torque and speed is possible with your unicycle, you are better using the power approach. The power available by human pedaling is between 200 and 400 W. Power § is always constant throughout the mechanical system, so:
P = T * w --> torque and angular velocity is the same for the crank and the wheel
P = Fc * Vc
P = Fw * Vw
So assuming a power of 300 W, if you travel at 8 mph (3.58 m/s),the wheel friction force is 83.8 N. With a 20" wheel (0.508 m), the torque is 21.29 N.m. The angular velocity is 14.1 rad/s (135 rpm). You can find the foot speed and force, knowing the crank radius. These equations are true for instantaneous values or average values.
Thank Saskatchewanian. He did the math, added the pretty colors and annotated it. I merely cut and pasted it.
Geoff
That is a nice chart, never seen it before, fits my experiences to a “t”.
Increasing crank length increases torque, but at a cost in terms of “ease of spin” and the akwardness that comes with having to manage a longer crank (pedal strike, sweet spot/power position, timing)
The only caveats I would add are rider experience/skills and tire size. I have found that both long and short cranks require more “work around” in terms of skill, so starting with cranks that are too long or too short could be a problem. In terms of tires, I was riding 165mm cranks on a 26 x 3 and did fine, but when I went to 26 x 3.8 I found my control and climbing was significantly reduced. I bumped up to a 170mm crank and my control and climbing returned to normal.
Starting muni 24" = 145-150mm, 26" = 150, 29" = 150-160, 36" = 150-165
All of my unis (26 x 3.8, 29 x 2.4, 36 x 2.5) are set up with 170’s, this is maybe not optimal for the 36, but I can’t find 175’s without q factor 
Saskatchewanian, thanks for the chart. I just ordered some 89mm cranks for my 24" club to act as a stopgap until I save enough for a 36" Coker.
I was in the process of doing the same thing but using LaTex for the equations and making tiny .pdf’s to make the equations look nice and pretty thank you for saving me from extra work I really didn’t need to do.
Wow, finally there is someone out there who likes longer cranks on a 36er than I do. I feel like an odd ball with my 165’s. I just switched to my “short” cranks, 152 mm, in preparation of racing season. They’re faster all right, but not so much fun riding on steep dirt roads and single track.
Geoff,
I’ve had my Schlumpf put together about a month. I’ve only had time to put about 20 miles on it. I’m running 137/165’s. These cranks are off of my 26" muni. I used the 165 hole for the Chilly Hilly in Feb. I had them on my N36er. At first I didn’t like them on the Nimbus. I have since got used to them. Now that I have a guni I will probably leave these cranks on it. Yesterday I hit 16 mph in high gear. I have not used the 137 hole since moving them over to the guni. In 1:1 I have really good control for cutting and zig zagging around people. My commute also involves alot of traffic. When I’m in heavy traffic I will run in 1:1. I am still getting used to high gear. I can shift ok. I don’t fall much but my shifting needs improvement. My feet are longer than the 165 cranks. My shoe size is 48 (14 US) I usually end up shifting with my ankle. I would prefer to use my heel.
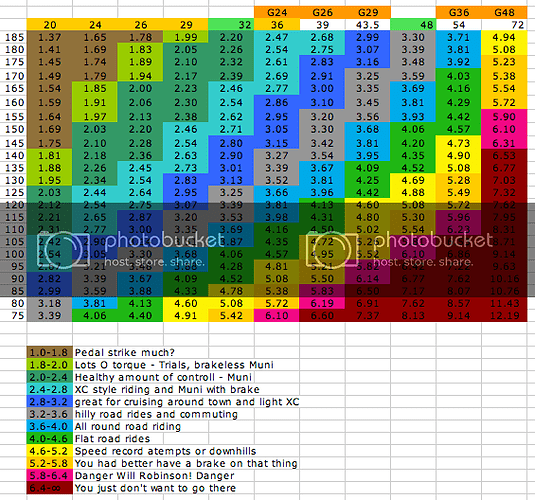
Something like this?
48 is about equal to 32 geared up.
I am planning to eventually build up a schlumpfable 48" so I added that to my chart.
Throwing a 32 in there fills the gap nicely eh?
And of course the chart is just a guideline. There are all sorts of other factors, like the fact that big wheels roll better than small wheels, big wheels have more momentum, the fact that I am scared of cranks shorter than 100mm… etc.
Ha! Magnificent. You’ve outdone yourself.
Geared 48?!?!?! Dude!
how fast could you go on a geared 48?
There are lots of variables here, and some of them are not easily quantifiable.
In terms of “gear ratio” the important thing is how far the unicycle moves for every inch your feet move.
This can be expressed as a ratio of the crank length to the radius of the wheel. As we’re dealing with lengths (rather than areas) it works just as well to compare the crank length with the diameter of the wheel, or even (should you choose) the circumference.
We’re used to thinking of cranks in millimetres, and wheels in inches.
For those of you who have forgotten, there are 25.4 millimetres in an inch.
As near as makes no odds, a 150 mm crank is 6 inches long.
Put 6 inch cranks on a 24 inch wheel, and the ratio of crank length: wheel diameter will be 1:4.
Now, put some 125 mm (5 inch) cranks on a 20 inch wheel.
Again, the ratio of crank length:wheel diameter will be 1:4.
In each case, if your foot moves an inch, the uni moves 4 inches.
And, in the short term, riding a 20 on 125 mm cranks, or a 24 on 150mm cranks will feel pretty similar.
But the big wheel will roll over bumps more easily. It will ahve more “flywheel effect” so it will be more stable.
On the other hand, the small wheel will be lighter and more manoeuvreable.
And the 1:4 ratio won’t work the same outside a certain range. As a thought experiment, consider riding a 1 inch wheel on 1/4 inch cranks. It won’t go as fast or as easily as the 20 on 125s!
Now as a thought experiment, try riding a 48" wheel on 12" cranks. Not easy.
On extremely short cranks, you are only using a tiny bit of the available muscle movement in your legs. On extremely long cranks, you won’t be able to move your legs smoothly in the huge circle.
But within common sense limits:
Big wheels go faster, but ar eharder to get up or down hill.
Short cranks go faster, but are harder to get up and down hill.
Mike, you need to cut your numbers in half. You need to use wheel radius instead of diameter.
152mm (6") cranks on a 24" wheel would be 2.0:1
127mm (5") cranks on a 20" wheel would be 2.0:1
The numbers on my chart represent the ratio between crank length and wheel radius (or virtual wheel radius).
And for those of you wondering, I do plan to eventually make a 48" wheel. It will be built with a regular 36h ISIS hub in such a way that I will have the option to swap that out with a Schlumpf if I want but probably never will. It’s fun to see what the numbers look like though. Why 48? because it is a nice round number, what you get if you mate 2 26" (559mm) rims end to end with a 2" tire and the biggest wheel I could use with long (175mm) cranks.
This is long term scheming, maybe next year, maybe the year after that, or maybe I will never get around to it at all. Geared 32 could be fun but my 32" wheel won’t ever get geared up unless a 32h hub shell becomes available for the Schlumpf hub.
I was wondering why, since “wheel_circumference = diameter * 2”, but then I remembered that “pedal_diameter = crank_length * 2”.:o
It really doesn’t matter. You are comparing linear measurements.
You can analyse the same problem in terms of crank:radius ratio of 1:2 or a crank:diameter ratio of 1:4.
You can even analyse it in terms of a crank:circumference ratio of 1: (4 * Pi) if you wish.
All of these will produce consistent results as long as you don’t change which statistics you are using part way through.
Double the radius, you double the diameter, you double the circumference.
It would be different if we were mixing lengths, areas, or volumes because then things change exponentially.
I deliberately chose crank length and wheel diameter simply because those are the figures that people use intuitively when thinking about unicycles.
To me it just makes more sense to match radius to radius, circumference to circumference etc. keeping it apples to apples. Ratios need to be the same measurement. Cranks are measured in radius, wheels are measured in diameter, either double the crank radius or half the wheel radius to get a direct ratio.
That way a 2:1 ratio would show that your tire moves twice as far as your foot, the force on the cranks is double the force of acceleration, etc.