Welches Modell hast Du ? ( GPS )
Ich habe einen BlackBerry Bold 9000
Bisher fahre ich mit folgenden Einstellungen:
36": 2827 mm Umfang = 90 cm Durchmesser
29": 2324 mm Umfang = 74 cm Durchmesser
Das schien bisher ganz gut mit Google-Earth überein zu stimmen.
Neulich ist mir allerdings ein eklatanter Unterschied zwischen großem und kleinem Gang aufgefallen. Da hat der Tacho den Hinweg bei Gegenwind durchgehend im kleinen Gang mit 24,5 km gemessen, den Rückweg bei 2/3 im großen Gang mit 22 km, das Ganze bei 36". Google-Earth sagt, es waren 24,3 km.
Die Tachowerte betrachte ich ohnehin als Circa-Werte, ich messe die Tour dann immer per Google-Earth nach.
Die Werte vom 26er decken sich ziemlich exakt mit den von mir gemessenen Werten.
Beim 29er sind sie anders, aber da hast du auch einen anderen Reifen auf einer anderen Felge.
Woher weiß dein Tacho, wie der Wind steht und in welchem Gang du fährst?
Realistisch könnte ich mir folgendes Vorstellen: auf dem Rückweg bist du schneller gefahren als auf dem Hinweg. Der Magnet ist relativ weit vom Sensor entfernt und es ist grenzwertig, daß das Vorbeiziehen des Magneten registriert wird. Bei höherer Geschwindigkeit und damit kürzerer Verweildauer des Magneten vor dem Sensor wurde dieses Ereignis manchmal nicht registriert, was dann zu einer kürzeren gemessenen Strecke führt.
Ich denke eher, dass ich im kleinen Gang gegen den Wind deutlich mehr Schlangenlinie gefahren bin. Und auf dem Rückweg im großen Gang (mit starkem Rückenwind, sodass es sich bei 24 km/h windstill anfühlte) ging es fast schnurgerade. Der Magnet ist nicht sehr weit außen montiert, bei etwas weniger als dem halben Radius. Da sollte es keine Probleme geben. Mit dem Fahrrad fährt man ja zuweilen deutlich schneller, und das kriegt der Tacho ja auch hin.
Ja, das könnte sein. Das führt aber zu einer weiteren Überlegung: bei mir liegt die Differenz zwischen Reifenumfang unbelastet und Reifenumfang belastet (wobei die Schlangenlinien gemäß Meßmethode berücksichtigt sind) beim 36er bei 2%, beim 29er bei 5%. Bedeutet das, daß ich mit dem 29er wesentlich stärkere Schlangenlinien fahre als mit dem 36er?
Falls sich 36er und 29er Reifen durch mein Gewicht ähnlich weit zusammendrücken, würde das bedeuten, daß ich auf dem 29er über 10cm Zickzack nach rechts und über 10cm Zickzack nach links fahre, also insgesamt über 20cm hin- und herwackle (siehe Berechnungen weiter unten). Das kann ich mir kaum vorstellen. Da würde man ja seekrank werden …
Die Schlangenlinien, die man mit dem Einrad fährt sind wohl ziemlich genau Sinuskurven (falls jemand anderer Meinung ist, bitte Einspruch erheben). Ich habe hier mal ein paar Werte ausgerechnet für die zusätzliche Länge der Schlangenlinie um 1m Weg zurückzulegen bei verschiedenen seitlichen Amplituden:
Amplitude: Länge
1cm: 0,250cm
2cm: 0,498cm
5cm: 1,239cm
7,5cm: 1,849cm
10cm: 2,455cm
15cm: 3,651cm
20cm: 4,827cm
Wenn ich also 1m fahre und dabei 10cm weit seitlich schlenkere (wohlgemerkt 10cm in jede Richtung ausgehend von der Ideallinie), muß ich 2,455cm extra fahren, habe also insgesamt 1,02455m zurückgelegt.
Für die mathematisch Interessierten, hier die Formel:
Wegstrecke = int_(t=0)^1 sqrt(1+a*(cos(2pit))^2) dt, wobei a die Amplitude ist.
Jetzt ist die Frage, wie viel Abweichung gegenüber dem unbelasteten Reifen vom Zusammendrücken herrührt, und wieviel vom Schlenkern. Wie bekommt man das raus? Vielleicht denselben Reifen auf ein Fahrrad montieren und auch da unter Last messen, wobei man nur rollen läßt und annimmt, daß man dabei überhaupt nicht schlenkert. Wer hat ein Fahrrad, in den ein 36er Rad reinpaßt?
Denksportaufgabe: wer findet den Rechenfehler? Ich korrigiere es dann morgen. Jetzt auf dem Handy ist mir das zu mühsam.
Muss ich das verstehen? Was hast du studiert? 
Andere Frage: Wer kann damit etwas anfangen
Die Wendes haben so ein Teil
Sum Sum
Ich fass es nicht…
Für die Formelinteressierte: Was heisst denn 1 sqrt? Strecke zum quadrat? Wir haben immer nur q geschrieben.
Das liest sich, als ob du den Tag damit verbringst solche Dinge auszurechnen, (statt ordentlich zu trainieren 
). Ich hoffe, dass du noch Zeit findest und auch fähig bist, frei von mathematischen Gedanken Einrad zu fahren. Ich versuche mal mir das vorzustellen - mmh, – muss ich mir Sorgen machen?
ach ja und dank dieses überaus detaillierten Threats bin ich ja fast versucht meinen TAcho wieder anzubauen oder mir mal einen ordentlichen zu leisten der es zuverlässiger tut. Denn bei dem alten habe ich vor einiger Zeit die Nerven verloren, weil er schon wieder mal nicht funktioniert hat.
@hugo: Genau. Mit Tacho fahren und mit google earth nachmessen reicht doch für den Hausgebrauch.
Und wenn ich mal meine Durchschnittsgeschwindigkeit messen möchte, mach ich das ganz altbacken mit bekannter Strecke und Zeiteisen oder Stoppuhr.
Um Strecken nachher am PC nochmal anschauen zu können, ist das GPS schon schön, aber Jogis portables GPS geht mir ziemlich auf die Nerven, weil der Akku schneller leer ist, als man das Gerät einschalten kann 
Es muß natürlich ( ) heißen
Wegstrecke = int_(t=0)^1 sqrt(1+a^2(cos(2pi*t))^2) dt
Damit ergibt sich dann folgende Tabelle:
Amplitude: Länge
1cm: 0,002cm
2cm: 0,01cm
3cm: 0,022cm
4cm: 0,004cm
5cm: 0,062cm
6cm: 0,09cm
7cm: 0,122cm
8cm: 0,16cm
9cm: 0,202cm
10cm: 0,25cm
15cm: 0,56cm
20cm: 0,993cm
30cm: 2,213cm
40cm: 3,887cm
50cm: 5,984cm
Das heißt, alles was unter 10cm Amplitude ist, kann man getrost vernachlässigen. Die Schlangenlinien haben also in der Praxis keinerlei Auswirkung auf die Wegstrecke.
sqrt steht für Quadratwurzel. Und das ^1 davor gibt die obere Grenze des bestimmten Integrals an. Formeln in Ascii zu schreiben ist halt leider nicht ganz einfach.
Aber hier gerne nochmal als Bildchen:
Eben nicht, deshalb muß ich es halt ab und zu in meiner Freizeit tun 
Aber irgendwas muß ja hängen bleiben, wenn man Mathe studiert hat.
Ja.
Nein.
Wie jetzt morgen? 
Nö! Man sollte bei der Kettenregel die Ableitung der inneren Funktion nicht vergessen. Insofern plädiere ich für:
Damit ergibt sich dann folgende Tabelle:
1 cm: 0,099 cm
2 cm: 0,394 cm
3 cm: 0,882 cm
4 cm: 1,561 cm
5 cm: 2,424 cm
6 cm: 3,464 cm
7 cm: 4,674 cm
8 cm: 6,045 cm
9 cm: 7,570 cm
10 cm: 9,238 cm
15 cm: 19,445 cm
20 cm: 32,066 cm
25 cm: 46,370 cm
30 cm: 61,860 cm
40 cm: 95,190 cm
50 cm: 130,489 cm
Für 2% Mehrweg hätte man dann ein Schlackern von 4-5 cm. Insofern schon signifikant und nach meinem Dafürhalten nicht unrealistisch.
Diese Ergebnisse decken sich auch besser mit einer Überschlagsrechung, die man durchführen könnte, indem man eine volle Sinusschwingung durch einen linearen Spline mit 5 Stützstellen approximiert und auf ein Blatt Papier malt. (Und dann mit dem Lineal nachmisst.) 
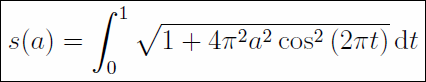
Wo du Recht hast hast du Recht.
Ja, aber bei dir ist das Rad grösser, da muss der Tacho mehr rechnen 
24,5km/h gegen den Wind??? Wieviele redundante Magnete hast du montiert?
Jetzt haben wir irgendwo ein Ständvermissnis! Ich habe die Stelle auf dem Boden markiert, wo das Einrad stand. Dann rollte ich es unbelastet eine Umdrehung weiter, machte einen zweiten Stich und mass den Abstand - so hatte ich den Umfang. Dann habe ich das Einrad wieder an den Ausgangspunkt gestellt und habe mich auf das Einrad hoch- und an der Wand langgezirkelt. Dann kam ich nach einer schlenkerfreien Radumdrehung 6 cm früher zum Stehen.
Das hat nun nichts mit dem Schlenkern und der Differenz zwischen Tacho und GPS zu tun. Dem Tacho habe ich den belasteten Umfang eingefüttert und damit sollte der jetzt korrekt messen was ich fahre.
Dann musste aber auch schreiben, wieso.
sqrt ist die Abkürzung für square-root, eben Quadratwurzel auf Englisch.
Wer lesen kann, ist klar im Vorteil: Ich schrieb gegen den Wind … 24,5 km. Nicht km/h. Was sagt das dem interessierten Leser? Es handelt sich um eine Entfernungsangabe, keine Geschwindigkeitsangabe. Ich schrieb dann im nächsten Post, dass ich zurüc bei Rückenwind 24 km/h schnell war. Und dafür braucht’s keine “redundanten” Magnete
Oh, ja, bei 24,5 km wird sich der Wind bemerkbar machen. Was gibt das dann? Ein Protestplakat für’s Guinessbuch?
Nee, hast ja recht. Da habe ich etwas geschusselt beim Lesen :o - so macht das alles Sinn.
(Korrektes) Lesen beruhrigt übrigens ungemein - genauso wie redundante Magnete!
Die Formel ist leider immer noch nicht richtig (ich sagte, doch, daß ich das erst heute korrigiere :D). Was bislang völlig unberücksichtigt blieb ist die Größe des Rades. Tatsächlich ergibt sich
int_(t=0)^1 sqrt(1+4a^2/d^2(cos(2pit))^2) dt
mit a=Amplitude und d=Durchmesser bzw. bei Einrädern mit Übersetzung d=Durchmesser*Übersetzung.
Ein Physiker hätte vorher ja auch direkt sehen können, daß etwas mit den Einheiten nicht stimmt.
Die Tabelle muß man nun also für unterschiedliche Setups getrennt betrachten. Ich habe das mal für mein 36er und mein 29er, jeweils im kleinen und großen Gang gemacht:
Amplitude: 36" kl. Gang; 36" gr. Gang; 29" kl. Gang; 29" gr. Gang
01cm: 0,01cm; 0,01cm; 0,02cm; 0,01cm
02cm: 0,05cm; 0,02cm; 0,08cm; 0,03cm
03cm: 0,11cm; 0,05cm; 0,17cm; 0,07cm
04cm: 0,20cm; 0,08cm; 0,30cm; 0,13cm
05cm: 0,31cm; 0,13cm; 0,47cm; 0,20cm
06cm: 0,45cm; 0,19cm; 0,68cm; 0,29cm
07cm: 0,61cm; 0,25cm; 0,93cm; 0,39cm
08cm: 0,79cm; 0,33cm; 1,21cm; 0,51cm
09cm: 1,00cm; 0,42cm; 1,52cm; 0,64cm
10cm: 1,23cm; 0,52cm; 1,88cm; 0,79cm
15cm: 2,73cm; 1,16cm; 4,15cm; 1,77cm
20cm: 4,79cm; 2,05cm; 7,22cm; 3,11cm
30cm: 10,4cm; 4,52cm; 15,4cm; 6,82cm
40cm: 17,6cm; 7,85cm; 25,7cm; 11,7cm
50cm: 26,1cm; 11,9cm; 37,5cm; 17,6cm
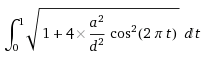
Wie hast du denn die Stellen am Boden exakt identifiziert? Bei dem Setup würde ich erwarten, daß du mehrere Zentimeter Meßungenauigkeit hast, weil es praktisch nicht möglich ist, auf dem Einrad sitzend “eine Umdrehung” präzise auszuführen.
Meine Methode sah folgendermaßen aus: Kreidemarkierung auf den Reifen, fahren, Abstand zwischen zwei auf den Boden abgefärbten Kreidepunkten messen. Dabei ist das Schlenkern berücksichtigt.